Research Theme: Persistent Gravitational-Wave Observables
This post summarizes two papers about three new procedures by which one can measure generalized notions of gravitational-wave memory. The first paper was an Editors’ Suggestion in Phys. Rev. D, and it had a synopsis published about it in Physics.
Papers Highlighted
-
A. M. Grant and D. A. Nichols. “Persistent gravitational-wave observables: Curve deviation in asymptotically flat spacetimes.” Phys. Rev. D 105, 024056 (2022), arXiv:2109.03832.
-
E. E. Flanagan, A. M. Grant, A. I. Harte, and D. A. Nichols. “Persistent gravitational-wave observables: Nonlinear plane wave spacetimes.” Phys. Rev. D 101, 104033 (2020), arXiv:1912.13449.
-
E. E. Flanagan, A. M. Grant, A. I. Harte, and D. A. Nichols. “Persistent gravitational-wave observables: General framework.” Phys. Rev. D 99, 084004 (2019), arXiv:1901.00021.
Summary of the Papers
 The gravitational-wave memory effect is often characterized by the lasting displacement it would cause between freely falling observers after a burst of gravitational waves pass by their locations.
Subsequently, it was realized that there other types of memory effects that freely falling observers could measure, including lasting relative velocities, changes in proper time elapsed, and relative rotation of inertial gyroscopes.
We were interested in determining procedures that observers could, in principle implement, by which observers could meaure all these memory effects (and potentially other new effects).
We in fact found three such types of procedures, which encompass the known memory effects, and potentially other new ones.
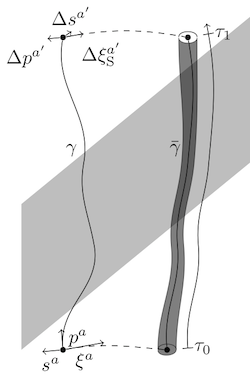
The first procedure involved measuring a type of deviation vector between two neary accelerating observers.
The second involves transporting a certain kind of linear and angular momentum around a closed curve in spacetime.
The third is based on measuring the location, linear momentum, and intrinsic angular momentum of a nearby spinning point particle.
We called the outcome of these measurement procedures “persistent gravitational-wave observables,” and we are currently investigating their properties in specific gravitational-wave spacetimes.
The gravitational-wave memory effect is often characterized by the lasting displacement it would cause between freely falling observers after a burst of gravitational waves pass by their locations.
Subsequently, it was realized that there other types of memory effects that freely falling observers could measure, including lasting relative velocities, changes in proper time elapsed, and relative rotation of inertial gyroscopes.
We were interested in determining procedures that observers could, in principle implement, by which observers could meaure all these memory effects (and potentially other new effects).
We in fact found three such types of procedures, which encompass the known memory effects, and potentially other new ones.
The first procedure involved measuring a type of deviation vector between two neary accelerating observers.
The second involves transporting a certain kind of linear and angular momentum around a closed curve in spacetime.
The third is based on measuring the location, linear momentum, and intrinsic angular momentum of a nearby spinning point particle.
We called the outcome of these measurement procedures “persistent gravitational-wave observables,” and we are currently investigating their properties in specific gravitational-wave spacetimes.
The first class of spacetimes that we investigated were the so-called nonlinear plane-wave spacetimes. We found that several observables can be obtained from the values of tensors that solve the equation of geodesic deviation (specifically for observalbes that involved geodesic curves). Thus, these observables contain information that is equivalent to the displacement and subleading displacement (e.g., spin or center of mass) gravitational-wave memory effects. However, for observables involving worldlines with acceleration, the persistent observables were more nontrivial (and nonlocal) functions of the solutions to the equation of geodesic deviation and the acceleration of the curve. This implies that there are much wider range of possible persistent observables than the leading and subleading displacement memory effects (which will be investigated in greater detail in future work).
We then investigated the curve-deviation observable in asymptotically flat spacetimes. At leading order in distance from the source, we found that there is an infinite hierarchy of memory effects when the curve-deviation observable is measured by observers with a nontrival, time-dependent acceleration. The entire collection of memory effects are sourced by “charge” and “flux” terms, where the flux part vanishes in the absence of gravitational waves. This charge-flux decomposition is well known for the displacement and subleading displacement (spin and center of mass) effects, but it was shown to hold for all of the acceleration-dependent effects in this paper. For the effects that depend on higher derivatives of the initial acceleration, the charge and flux sources are more and more subleading parts of the expansion of the spacetime metric and curvature in a series in inverse distance. Thus, the curve deviation observable is capable of probing very high-order persistent changes in the spacetime through a measurement at large distances. This type of asymptotic reconstruction of the interior of a spacetime is reminiscent of the types of holography that appear in high-energy physics and string theory.
