Research Theme: Definitions of (super) angular momentum in asymptotically flat spacetimes
This post highlights a paper and essay that investigates several commonly used definitions of angular momentum and super angular momentum in asymptotically flat spacetimes and the differences in the values of the (super) angular momentum predicted by these definitions for binary-black-hole mergers.
Papers Highlighted
-
A. Elhashash and D. A. Nichols. “Definitions of (super) angular momentum in asymptotically flat spacetimes: Properties and applications to compact-binary mergers.” Phys. Rev. D 104, 024020 (2021), arXiv:2101.12228.
-
G. Compere and D. A. Nichols. “Classical and Quantized General-Relativistic Angular Momentum,” (2021). arXiv:2103.17103.
Summary of the Papers
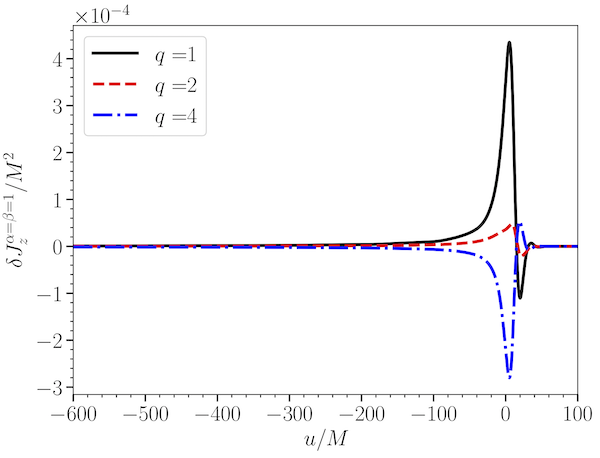
Finding a definition of the angular momentum of an isolating gravitating system has a long and involved history. Over several decades of (sporadic) work on the topic, a number of different researches used different methods to converge on an expression for the quantity. However, there were still several different definitions used in different subfields, which were not clearly equivalent. It was subsequently noted that there are in fact a two-parameter family of angular momenta that generalize many of the existing definitions. This two parameter family satisfies a number of physically reasonable conditions.
With UVA graduate student Arwa Elhashash, we found that one condition that the two-parameter family did not satisfy was that it vanished in flat spacetime. Imposing this requirement forced the two parameters to be equal, which left a one-parameter family of angular momentum (and the different definitions used in the various subfields were all consistent with this one-parameter family). We then explored how large the difference in definitions is for binary-black-hole mergers. For nonspinning binaries, the difference in the (orbital) angular momentum for the definitions is illustrated in the figure above. The figure shows that the definitions agree at early times and after the gravitational waves pass, but there is a difference when the system is radiating gravitational wave most strongly. The difference is also largest for equal mass ratios (q=1). We also investigated a one-parameter family of super angular momentum, a kind of generalization of angular momentum. For the super angular momentum, there is again a difference between the definitions, but this difference lasts after the gravitational waves have passed (which occurs because of the graviational-wave memory effect). The amplitude of the differences in the (super) angular momentum are small, but they can be resolved by numerical simulations of binary-black-hole mergers.
I also wrote an essay for the 2021 Gravity Research Foundation Essays on Gravitation competition with Geoffrey Compere. The subject of the essay was the definition and transformation properties of angular momentum and its generalizations in asymptotically flat spacetimes. We discussed the fact that the most-frequently used value in the one-parameter family of angular momentum (that which reduces to the Komar formula when there is an exact rotational symmetry) is not the same value of the angular momentum that gives rise to the standard charge algebra for the super angular momentum. We also noted that there are a wider range of possible definitions of angular momentum and its generalizations beyond the one-parameter family discussed above, including those which behave like an intrinsic angular momentum that does not transform under (super)translations.
