Research Theme: Hybrid Post-Newtonian and Black-Hole Perturbation Model
This post is a summary of two papers I wrote with Yanbei Chen during my Ph.D. about a semi-analytical model for explaining the properties of the gravitational waveforms from binary-black-hole mergers.
Papers Highlighted
-
D. A. Nichols and Y. Chen. “Hybrid method for understanding black-hole mergers: Inspiralling case.” Phys. Rev. D 85, 044035 (2012), arXiv:1109.0081.
-
D. A. Nichols and Y. Chen. “Hybrid method for understanding black-hole mergers: Head-on case.” Phys. Rev. D 82, 104020 (2010), arXiv:1007.2024.
Summary of the Papers
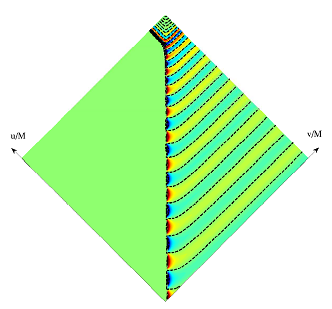While it is now feasible to compute the merger of black holes with large-scale simulations, it is still helpful to use analytical methods to develop faster ways of calculating gravitational waveforms and to provide intuitive understanding of these processes.
We put forward a method of combining two analytical approximation schemes—Post-Newtonian (PN) and black-hole-perturbation (BHP) theories—to make approximate gravitational waveforms and to clarify the structure of a black-hole-binary merger.
The central idea of the method is to use both PN and BHP theories simultaneously at a given time, but to restrict their use to spatial regions where either they are good approximations or their errors will not effect important observables like the gravitational waveform.
Typically, PN and BHP theories are applied to the entire spatial region of distinct times in the evolution of a binary.
Applying both PN and BHP theory at once requires there be a region where one can match the two theories. We found empirically that we can match the theories at the locations of the PN theory’s point particles. We then let the matching region evolve by requiring that the point particles follow a combination of geodesic motion in the final black-hole’s background and dissipative motion from a radiation-reaction force (which was calculated self-consistently from the emitted gravitational waves). This new set of evolution equations simultaneously computes the matching region and the gravitational waves outside of it. The waveform that they produce is not calibrated to numerical simulations, but still agrees rather well with them for both head-on and quasi-circular binaries. The method was also useful for exploring how black holes get large recoil velocities when they have spin vectors that are anti-aligned in the orbital plane.