Research Theme: Extended BMS Symmetries, Spin, Center-of-Mass and Higher Memory Effects

This post summarizes five papers related to the conserved quantities of extensions of the Bondi-Metzner-Sachs (BMS) group and related higher memory effects.

Papers Highlighted

• S. Siddhant, A. M. Grant and D. A. Nichols. “Higher memory effects and the post-Newtonian calculation of their gravitational-wave signals,” (2024). arxiv:2403.13907

• E. E. Flanagan and D. A. Nichols. “Fully nonlinear transformations of the Weyl-Bondi-Metzner-Sachs asymptotic symmetry group.” J. High Energy Phys. 03, 120 (2024) arxiv:2311.03130.

• D. A. Nichols. “Center-of-mass angular momentum and memory effect in asymptotically flat spacetimes.” Phys. Rev. D 98, 064032 (2018), arXiv:1807.08767.

• D. A. Nichols. “Spin memory effect for compact binaries in the post-Newtonian approximation.” Phys. Rev. D 95, 084048 (2017), arxiv:1702.03300.

• E. E. Flanagan and D. A. Nichols. “Conserved charges of the extended Bondi-Metzner-Sachs algebra.” Phys. Rev. D 95, 044002 (2017), arxiv:1510.03386.

Summary of the Papers

The Bondi-Metzner-Sachs (BMS) group is the symmetry group of asymptotically flat spacetimes, and it consists of the Lorentz transformations and the supertranslations (an infinite-dimensional commutative group that has the spacetime translations as a subgroup). There recently was a proposal that a larger symmetry algebra than the BMS algebra could be relevant. This new algebra was called the extended BMS algebra, and it included the infinite number of conformal Killing vectors on the two-sphere, not just the smooth six-parameter family of Lorentz transformations. Eanna Flanagan and I computed the conserved quantities corresponding to these new symmetries in a somewhat more general context than before, and we found that they are finite and that they have an electric- and a magnetic-parity part. These two parts are generalizations of the spin angular momentum and the center-of-mass parts of the relativistic angular momentum (the superspin and super-center-of-mass charges, respectively). The change in the superspin charges can be a source of a new kind of memory effect, which had been proposed earlier, called the spin memory effect.

Much later, Eanna Flanagan and I computed the transformation properties of the metric functions in the BMS formalism under different classes of fully nonlinear coordinate transformations. We were able to compute, and slightly generalize, the form of a vacuum solution under a new set of symmetry transformations known as the Weyl BMS group. These expressions for the transformations of the metric functions will prove useful in understanding how the conserved quantities in the BMS, generalized BMS and Weyl BMS transform under the respective class of symmetry transformations.

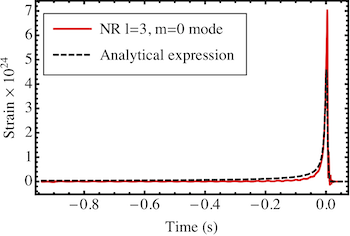
Returning to the spin memory effect, another source of it is the effective angular momentum per solid angle that is radiated in gravitational waves. I computed the expansion of this effective angular momentum flux in terms of radiative moments of the gravitational-wave strain, thereby deriving a quadrupole-like formula for the spin memory. I then specialized to compact binary sources in the post-Newtonian approximation. In this limit, I found that the spin memory has a substantial slow secular growth during the inspiral stage of a compact binary. In addition, the rate of accumulation of the spin memory is related to a non-hereditary, nonlinear, and non-oscillatory contribution to the gravitational waveform that appears at a high order in the post-Newtonian expansion. This rate of accumulation of the spin memory might be detectable by third-generation gravitational-wave detectors, such as the Einstein Telescope, by coherently adding the spin memory signals from hundreds of gravitational-wave observations of black-hole-binary mergers.

I also showed that changes in the super-center-of-mass charges can also produce a new type of memory effect, which I called the center-of-mass memory effect. Like the spin memory effect, it produces a lasting change in a quantity related to the time integral of the gravitational-wave strain. There are terms in the gravitational waves related to the center-of-mass memory effect. These gravitational-wave terms, however, will be weaker than those related to the spin memory effect. As a result, it is less likely that the next generation of gravitational-wave detectors will be able to find evidence for the effect. It should, however, appear in the post-Newtonian expansion of the gravitational waveform, when the gravtiational waveform is computed at fourth post-Newtonian order.

Most recently, Siddhant, Alex Grant and I completed an investigation of the gravitational-wave memory effects related to the higher temporal moments of the news tensor (the time derivative of the gravitational-wave strain). We identified gravitational-wave signals related to these moments of the news, and computed several properties of these so-called higher memory effects. First, we developed a systematic procedure to compute the higher memory effects from a sequence of nonlinear flux-type terms and a charge-type term. Next, we performed a multipolar expansion of the first three flux-type terms; the first two sets of flux terms reproduced the multipolar expansions of the displacement, spin and center-of-mass memory effects; the third set of flux terms had not been investigated before. These new terms, named the ballistic memory by Alex, were our main focus for performing computations from compact-binary sources. Finally, we worked in the post-Newtonian approximation, and we found that one such term flux term was of the same post-Newtonian order as the spin memory effect. Given that the spin memory could be detected by the next-generation of ground-based gravitational-wave detectors, this part of the gravitational-wave signal looked like the most promising signature of a new higher memory effect that could be detected.